A quick
(equation free)
intro to Hidden Markov Models applied to Stock Volatility
Luis Damiano
R/Finance 2017 | May 19
Motivation
Ever heard this question?
How’s the market today?
Possible answers
- Trader: bullish/bearish
- Risk analyst: low/high volatility
- Behavioural finance: risk on/off
- Macro economist: expansion/recession
How’s the market today?
This fair question has an implicit assumption:
Markets
DON’T
behave
exactly
the same way
every single day.
Markets have states instead
But they’re
HIDDEN
- can’t be observed directly
- need inference based on observed data (prices, volume, order size)
Hidden Markov Models
Specification
HMM involves two interconnected models
- State model: discrete-time, discrete-state Markov chain with hidden states.
- Observation model: a model for the observations, emissions or output.
- Keywords: bayesian inference, probabilistic machine learning, state space models.
All models are wrong, but some are useful. (George E. P. Box)
HMM and Mixtures
HMM may be interpreted as an extension of a mixture model
- Each single time slice corresponds to a mixture, but…
- The component for each observation has memory.
HMM applied to stock vol!
Setup
- Goal: modeling deterministic volatility for stocks
- Data: Daily close prices 2011-2016 from ^GSPC, F, GM, THO, AIR.
- State model: binary latent state with first-order markovian memory
- Observation model: \(GARCH(1, 1)\)
One stock (F) with two latent states
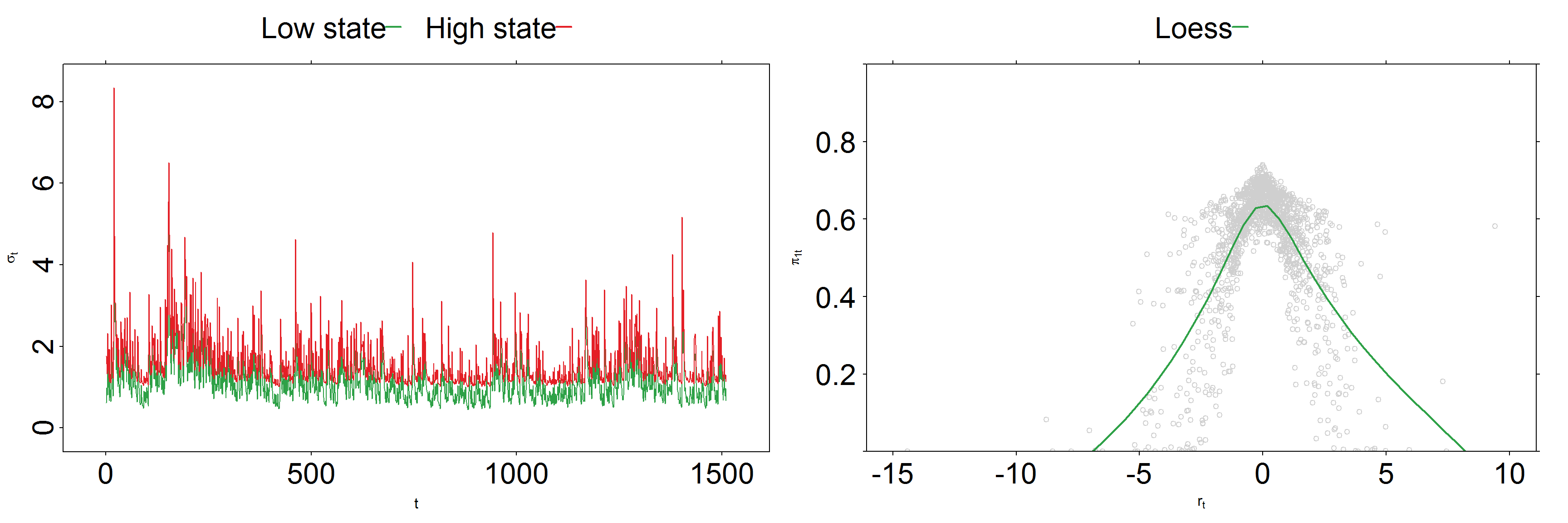
Common sense check: Observing small returns makes us more confident about using the low volatility model.
A stock portfolio with two latent states
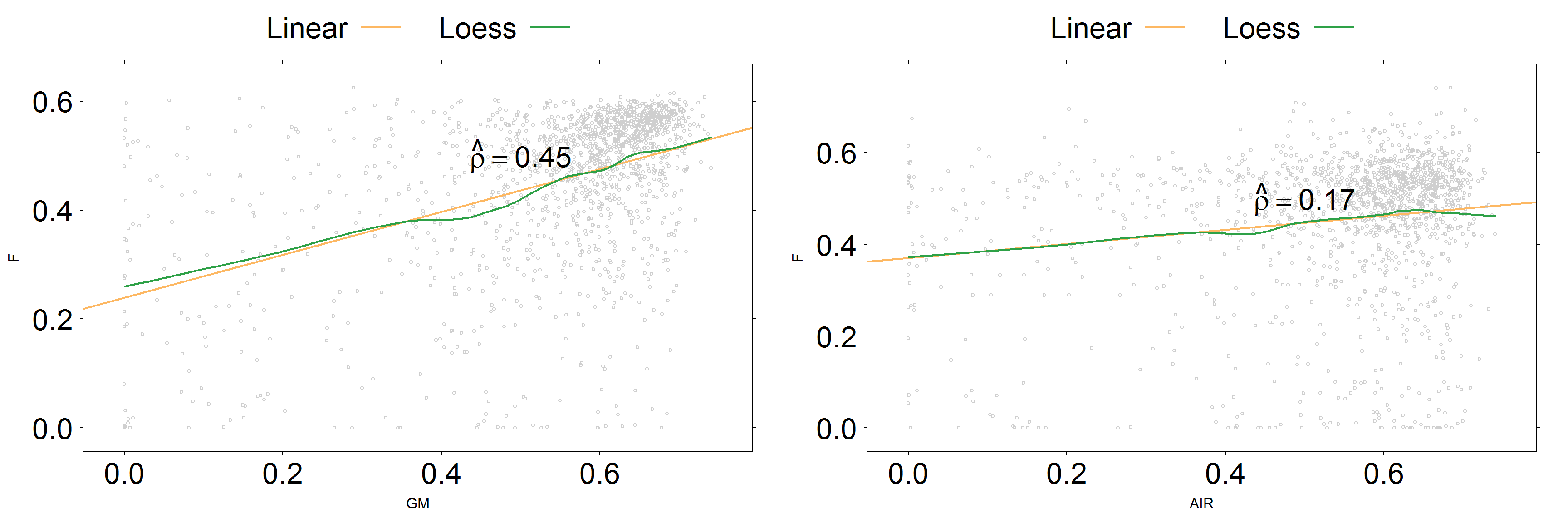
Correlation in belief states is higher for stocks in the same industry (compare F/GM vs F/AIR).
Takeaway
- States are hidden, yet meaningful. They are subject to useful domain knowledge interpretation.
- Belief states across assets are cross-correlated.
- This relationship is stronger for stocks in the same industry, with similar business models or similar exposure to macroeconomic factors.
Further research
What if hidden states were hierarchical?
Risk state of a global portfolio may be mapped into components
\(\text{Country} + \text{Industry} + \text{Individual}\)
I’m currently exploring
Hierarchical Hidden Markov Models applied to finance
for my Google Summer of Code 2017 project.
Thanks!
May any of these ideas be of value for your trading strategy or risk model?
Check the extended material for this talk
(R Notebook, fully working code, references and neat plots)
https://github.com/luisdamiano/rfinance17